[난그댄!] 모티프와 엔트로피
여러분 안녕하세요. 이제는 날씨가 오락가락하지만 영하의 날씨도 오는 요즘입니다. 지난 연재에서 우리는 DNA/RNA/Protein 서열들에서 반복적인 패턴이 나타날 때 효과적으로 시각화해 주는 시퀀스 로고(sequence logo)를 배웠습니다. 제가 계획했던 3가지 방식 중 벌써 2가지인 Position Frequency Matrix (PFM)과 Position Probability Matrix (PPM)을 배웠습니다.
이들도 많이 쓰이긴 하지만 ‘여기 시험에 나옵니다. 중요하니 별 3개 그리세요’라는 느낌이 없는 단점이 있습니다. 즉, 한 번에 봤을 때 어떤 부분에서 어떤 구성요소가 중요한지 ‘강조’ 되지 않는다는 것이지요. 효과적인 플랏/그래프는 긴 Figure legend가 없을 정도로 직관적으로 전달돼야 합니다.

그림 1. (위) PPM 방식의 시퀀스 로고, (아래) ICM 방식의 시퀀스 로고
지난 연재에서 우리는 PFM과 PPM을 만드는 것을 배웠습니다.
자세한 내용은 이전 것을 참고하시고 이제 한 단계를 넣어 봅시다.
그것은 정렬된 위치 별로 엔트로피(entropy)를 고려하는 겁니다. 이 과정을 거치면 그림 1의 2번째 그림과 같이 나타나게 됩니다.
여기서 말하는 엔트로피는 정보이론의 아버지인 클로드 섀넌(Claude Elwood Shannon)이 도입한 개념으로 ‘무작위 변수가 가지는 평균적인 정보량’을 의미합니다. 한 줄로는 이해가 어려울 테니 세세하게 풀어봅시다.
x라는 이름의 복권을 우리가 여러 장을 구매했다고 가정해 봅시다. 이때, 우리에겐 당첨 복권이 있을 수도 있고 없을 수도 있습니다. 하지만, 확실하게 아는 것은 당첨 복권의 확률은 매우 낮다는 것이죠. 복권의 당첨액은 생각하지 말고 당첨 확률은 백 분의 일(1/100)으로 생각해봅시다. 이를 수학적으로 쉽게 표현하기 위해 x=1은 당첨을 의미하고 x=0은 꽝이라 정의하겠습니다. 그럼, 당첨과 꽝은 아래와 같은 수식으로 표현됩니다.

이제 우리가 복권의 당첨가치를 매긴다고 생각해 봅시다. 일반적으로 철에 비해 황금이나 리튬 등은 매우 희소하기 때문에 가치가 높습니다. 이와 마찬가지로 복권 역시 희소할수록 가치가 크다라고 정의할 수 있을 겁니다. 이를 이용하면, 복권들의 가치는 확률에 로그 (log)를 취한 후 음수를 곱해서 희소함에 비례하게 매길 수 있게 됩니다.
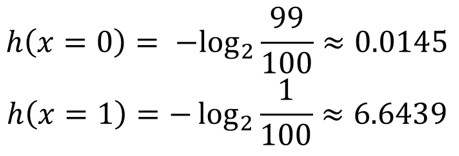
여기서, 로그의 지수를 2로 한 것은 관습적인 표기법으로 어떤 것을 사용하셔도 무방합니다. 이 가치의 단위를 섀넌은 binary digits의 약자를 따서 Bits라고 정의했습니다. 그래서, 아래 그림에서 y축 단위가 Bits로 나오게 된 것입니다.

그림 2. ICM방식의 시퀀스로고 [출처 1]
이러한 상황에서 우리가 얻을 수 있는 평균적인 가치가 어떻게 되는지 알아봅시다. 학창 시절 우리가 확률과 기댓값이란 것을 배울 때를 회상하면 쉽게 풀 수 있습니다.100원짜리 동전을 던져서 앞면이 나오면 돈을 따고 뒷면이 나오면 돈을 잃는다는 간단한 문제를 예로 들겠습니다. 이 경우, 우리의 기대수입은 앞면이 나올 확률이 1/2이므로 50원이라는 것을 알 수 있습니다. 이를 활용하면 우리가 얻을 수 있는 평균적인 가치값을 알 수 있습니다.

이것이 엔트로피를 구하는 공식입니다. x 복권을 서열의 위치에 대응시키고 당첨 여부는 4가지 염기서열 또는 20가지 아미노산으로 바꾸게 되면 위의 공식을 통해 서열의 각 위치 별 정보량을 알 수 있게 됩니다.
여기서, 말하는 엔트로피 정보량은 불확실성 (uncertainty) 또는 비균질성에 관한 내용입니다. 엔트로피는 원소들이 균등분포에 가까울수록 커지는 경향이 있기 때문입니다. 즉, 이것의 값이 클수록 해당 서열 위치에서는 특정한 염기/아미노산 선호가 없다는 것을 의미합니다. 따라서, 각 위치의 중요도는 아래의 수식으로 표현됩니다.

여기서 N은 변수 x의 가짓수를 의미하며 일반적으로 아미노산의 경우 N=20, 염기서열은 N=4가 됩니다. IC는 Information content로 해당 위치 x에서의 정보량 (중요도)를 의미하게 됩니다. IC값이 크면 클수록 해당 위치에서 특정 원소에 대한 선호가 강하게 나타난다는 것을 의미하게 됩니다. 앞에 log2N이 들어가는 것은 완벽한 균등분포 상황일 때의 불확실성을 표현하기 위해 넣는 것입니다. 이를 통해 각 위치들의 중요도를 정량화할 수 있게 됩니다. 균등분포에 가까울수록 IC(x) 값은 0에 가까워지게 됩니다.
이제 마지막으로 각 위치 내의 각 구성원소의 중요도는 아래의 수식으로 계산하면 ICM방식으로 시퀀스 로고를 그리기 위한 준비는 끝납니다.

여기서 n은 아미노산 또는 염기의 구성요소를 의미하고 x는 서열 내 위치를 의미합니다. P(n,x)라는 것은 x위치에서 n이라는 요소가 나올 확률을 의미하는 것입니다. 위치 중요도인 IC(x)는 해당 위치에서의 구성 원소들의 분포로 결정되기 때문에 확률을 곱해서 각 원소 별로 가중치를 분배해 주는 것입니다.
이 방식을 이용하면 그림 2에서 위치 5번은 위치 1번에 비해 약 2배 정도 정보량을 가지고 있다고 할 수 있습니다. 물론, 그렇게 표현하는 경우는 없습니다만 상대적 중요도는 명확하게 시각화할 수 있게 됩니다. 아래 그림 3은 실습데이터에서 실제 계산된 IC(x)값을 가지고 그린 막대그래프와 IC(n,x)까지 계산된 결과로 그린 시퀀스로고입니다.
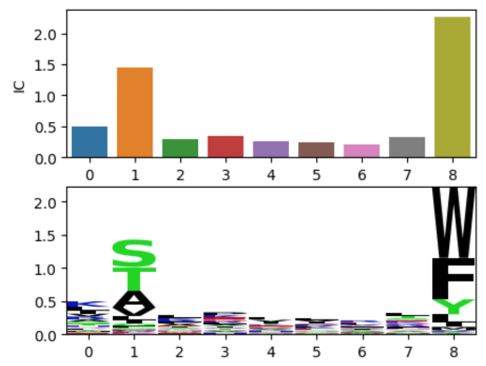
그림 3. IC(x)와 시퀀스로고
그림 3과 같이 8번과 1번 위치가 다른 위치들에 비해 중요하다는 것이 보이실 겁니다.
PPM이나 PFM으로 그릴 때보다 보다 직관적이지 않으신가요?
최대한 쉽게 설명하려 했지만, 수학적인 부분이 많이 나와서 잘 이해가 안 되는 부분도 있을 겁니다. 제공되는 실습자료를 확인하시는 한편 질문을 남겨주시면 답변드리도록 하겠습니다.
수고하셨습니다.
노트북 : https://colab.research.google.com/drive/1VWYnXszYTMTz-1UBZgMNActP6UWxVXFG?usp=sharing
출처
[1] https://www.nature.com/articles/s41467-023-40220-1/figures/2
본 기사는 네티즌에 의해 작성되었거나 기관에서 작성된 보도자료로, BRIC의 입장이 아님을 밝힙니다. 또한 내용 중 개인에게 중요하다고 생각되는 부분은 사실확인을 꼭 하시기 바랍니다.
BRIC(ibric.org) Bio통신원(뉴로(필명)) 등록일2023.12.15